Prerequisites

Note

Quantum computing can be complex and difficult to understand. But we're going to show you that even if you don't know anything about it, it's possible to do many things by learning a few basics without looking too far.

This page is a tutorial / lesson to help you understand the main concepts of Quantum circuits applied to computers. This part of the documentation is mostly theoretical but it will make your grasping of Quantum Nodes easier.

Qubits

What are Qubits?

Quantum Nodes is an addon working with notions of quantum computing, where we use “qubits”.

As its name suggests, it derives from “bit” used in “classic” computing. However qubits work differently.

The bit is binary, which means that it has only two possible states: on or off (0 or 1).
The qubit, on the other hand, carries much more information. As a bit, qubit can transmit a state being 0 or 1.

But the difference with qubits is that their state is not “static”. Indeed, as long as a qubit is not measured (in other words as long as it is not observed), it's sometimes impossible to determine in which state it is.

What does it mean?

A qubit is based on elements acting according to the principle of Schrödinger's cat experiment. This experience explains that an element not observed can be in one state, in another state or in both states at the same time (then we say that the element is in superposition). It's only when the element is observed that it loses this state of superposition and “chooses” a definitive state according to certain probabilities.
Here, we exploit the superposition of qubit to obtain information about the probabilities of states they can be. So, a qubit, as long as it is not measured, carries the probabilities of being in one state or another (0 or 1).

Note

To resume, the state of a qubit can be 0, 1 or (0: x% and 1: y%) as long as it's not measured.
Then we can see qubits as vectors of probability [x% , y%], we call it “state vector”. This representation is very useful to calculate with qubits in superposition.
To be able to manipulate qubits, we prefer to use complex numbers to control their “phase” (concept that we will see later).

Using multiple qubits

Just like bits, qubits are combined to make a result. In the same way, we align qubits to obtain a sequence of 0 and 1. | However, as we have seen previously, qubits sometimes have undetermined states, so we obtain the probability to get multiple sequences.

Example with 3 qubits:

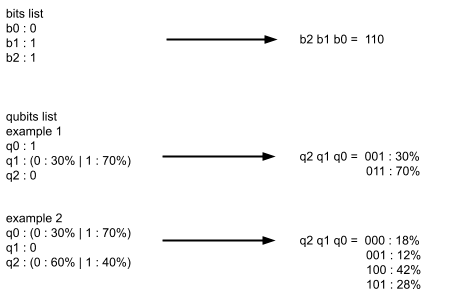
In the same way that 3 bits can compose 23 = 8 possible sequences, 3 qubits can compose 8 possible sequences. | However bits are static, once in a state it composes only one possible sequence, while qubits are sometimes not determined, they can give several different results according to the probabilities of qubits.

Note

Note that the order of a sequence starts with the last qubit and ends with the first, as for bits.

In example 1, we have 3 qubits: 1 is in superposition and 2 are fixed by initialization or by measurement (we will develop this point later). | We notice in result that we can obtain 2 possible sequences with different probabilities.

In example 2, 2 qubits are in superposition and 1 is fixed. We then have 4 possible sequences. It's easy to observe that the probability of results inherits the probability of the qubits.
What we can learn from these examples is that qubits can carry several results in a single calculation, while bits can only transmit one sequence at a time.
So it's possible with qubits to give several solutions to a requested calculation in a single operation.

Quantum entanglement

The principle of entanglement is not very well understood by scientists. | However, we can retain that quantum entanglement allows two qubits to influence each other by sharing information regardless of their distance in space.

Important

In other words, once two qubits are entangled, they are dependent on each other.

Then we can imagine different ways to transform qubits with the state of another qubit.

This particular property is used by some “quantum gates”.